

There's no real number that when you multiply it by itself you get the answer 144. A radical is a number that has a fraction as its exponent. Generally speaking, it is the process of simplifying expressions applied to radicals. This is no real solution, no real number. Simplifying radicals is the process of manipulating a radical expression into a simpler or alternate form. It's like I square rooted 144 and then negativize it, as opposed to this: The square root of 144, if you try it on your calculator, you'll see it says "Error". The negative square root of 144 would be 12. The negative square root of 144 is not the same thing as the square root of 144. One last thing, I want to leave you with before you start your homework problems is to watch out for this property. Get really comfortable with all the squares of the numbers one through 15, so that when you're doing these problems, you can recognize these factors. Pretty much, you just have to memorize these.
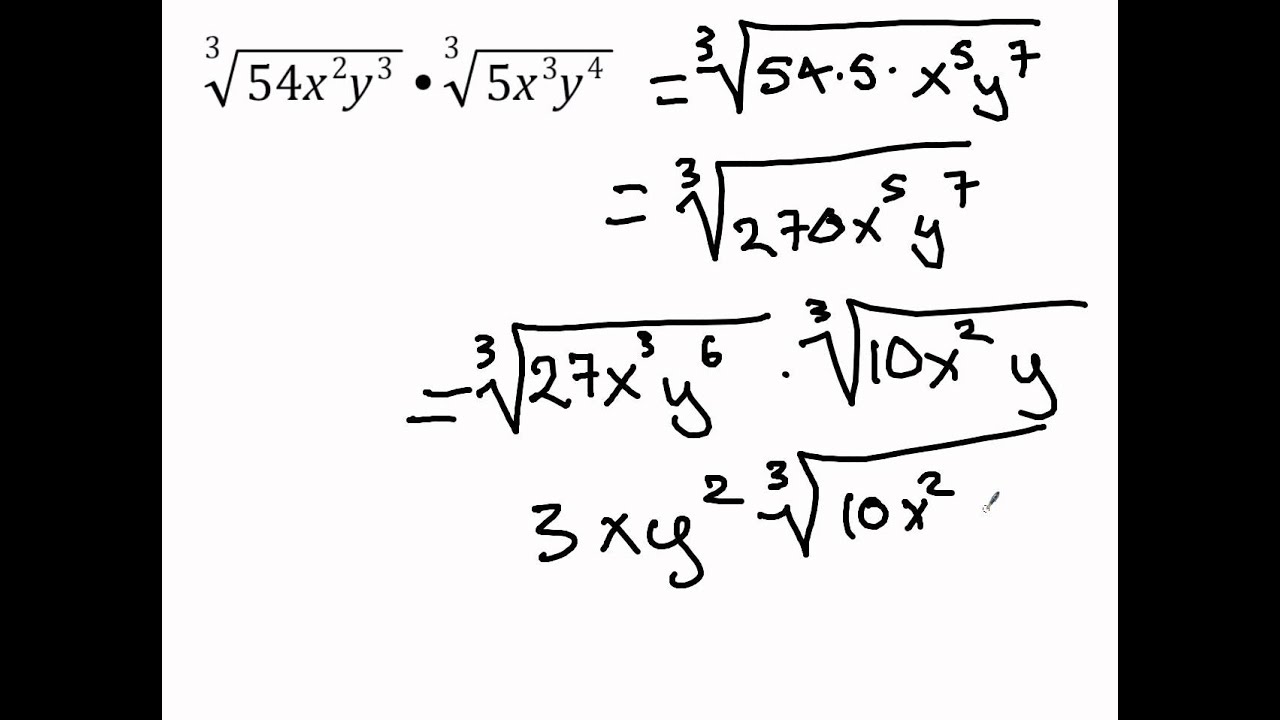
I've gone through and listed all of the perfect squares for the numbers one through 15, like one times itself is one, two times two, three times three, four times four. So when you're approaching these problems, it's really important that you're good at recognizing perfect square factors. Simplified form means there are no perfect factors in the radicand, or no square numbers under the "square rootie", if that makes more sense to you. This would be my answer in simplified form. So the simplified form of the square root of 18 would be, let's see, square root of nine is three, times the square root of two. I don't know what the square root of 18 is, but I do know that 18 is the equal to the product of nine times two. This decimal times that decimal gives me that answer.Īnd sometimes it doesn't make a whole lot of sense if you don't have a calculator handy, but it can be really useful in problems like this, like the square root of 18. These pairs of terms can be combined: The same process will work with variables, and it will also work with cube roots. Heres an example: Simplify the expression. Of course, we wont always have like radicals when we simplify, but when we do, we can combine them. It's going to be a tiny bit off because I'm rounding, but you guys get the idea. This expression can be simplified by first simplifying each individual term. Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions.
#Simplify radical expressions free
And I'm claiming that 3.16 is equal to 1.41 times whatever the square root of five is 2.23. Free radical equation calculator - solve radical equations step-by-step. The square root of two is the decimal 1.41. Find the radical index, and for this case, our index is two because. Find the prime factors of the number inside the radical. Simplify by multiplication of all variables both inside and outside the radical. The square root of 10 is the decimal of 3.16. Simplify the expressions both inside and outside the radical by multiplying. If you don't trust me, grab yourself a calculator and check it out. The square root of 10 is equal to the square root of two times the square root of 5. If I had the square root of 10, that's not something that you guys have probably worked with very much. This is only true as long as A and B are both positive and not 0.
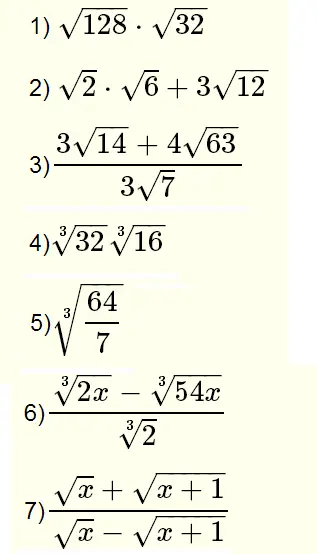
It's equal to the square root of A times the square root of B. So when you're asked to simplify radical expressions, we have a really important property and here's what it is: If you have the square root of the product AB that's equal to the product of their individual square roots. And you'll see that more when we start doing some problems.

So the other thing is that the thing that's under the radical sign, or under the "square rootie" is called a radicand. Radical expression just means it's an expression that has a square root sign. When you guys start working with radical expressions, it's important that you know what a radical expression is.


 0 kommentar(er)
0 kommentar(er)
